Home » Random matrices » Monotonicity of Lyapunov exponents

Monotonicity of Lyapunov exponents

Let $A$ be a square matrix with non-negative entries, such that the entries of $A^TA$ are positive.
A nice example to start with is

$A=\begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} \,.$

Given $p \in (0,1)$ , consider a random matrix product

$Y_n=M_1\cdots M_n$

where the $M_k$ are independent, and
for each $k$ ,

$\mathbb P_p(M_k=A)=p \quad \text{and} \quad \mathbb P_p(M_k=A^T)=1-p \,.$

Fix a
submultiplicative norm $\| \cdot\|$ on $d \times d$ matrices, e.g. the operator norm

$\|M\|=\sup_{\|x\|_2=1} \|Mx\|_2 \,,$

where the supremum is over vectors $x$ in the unit sphere of
${\mathbb R}^d$ . The sequence $E_p(\|Y_n\|)$ is submultiplicative, i.e.

$\forall m,n \quad E_p(\|Y_{m+n}\|) \le E_p(\|Y_m\|) \cdot E_p(\|Y_n\|)\,,$

so by Fekete’s lemma, the limit

$L(p):=\lim_{n \to \infty} \frac1n\log E_p(\|Y_n\|)$

exists; it is called the top Lyapunov exponent for this matrix product, and was
first studied in [1]. In [2], it was shown that $L(p)$ is a real analytic function of $p$ .

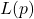(a) Does $L(p)$ attain its maximum at $p=1/2$ ?
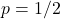(b) Is 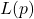$L(p)$ nondecreasing in $(0,1/2]$ ?

[1] Furstenberg, Harry, and Harry Kesten. "Products of random
matrices." The Annals of Mathematical Statistics 31, no. 2 (1960):
457-469.

[2] Peres, Yuval Analytic dependence of Lyapunov exponents on
transition probabilities. Lyapunov exponents (Oberwolfach, 1990), 64–80,
Lecture Notes in Math., 1486, Springer, Berlin, 1991.

Monotonicity of Lyapunov exponents

Send me questions about this open problem

Contact Me