Home » Diophantine analysis » Uniform dilations modulo a prime

Uniform dilations modulo a prime

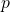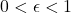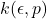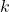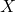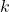For $p$ prime and $0<\epsilon<1$ , let $k(\epsilon,p)$ be the minimal integer $k$ such that for any set $X$ of $k$ distinct rationals in 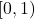$[0,1)$ with the same denominator 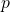$p$ , there exists an $\epsilon$ -dense dilation 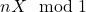$nX \mod 1$ .

How does 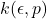$k(\epsilon,p)$ grow when $\epsilon$ decreases? The best bounds known [1] are

$\frac{c}{\epsilon} \log (1/\epsilon) \log \log \log(1/\epsilon) \le k(\epsilon,p) \le \frac{C}{\epsilon^2}$ .

REFERENCES

[1] Alon, Noga, and Yuval Peres. "Uniform dilations." Geometric & Functional Analysis GAFA 2 (1992): 1-28.

Uniform dilations modulo a prime

Send me questions about this open problem

Contact Me